Convolutional NLOS Operator

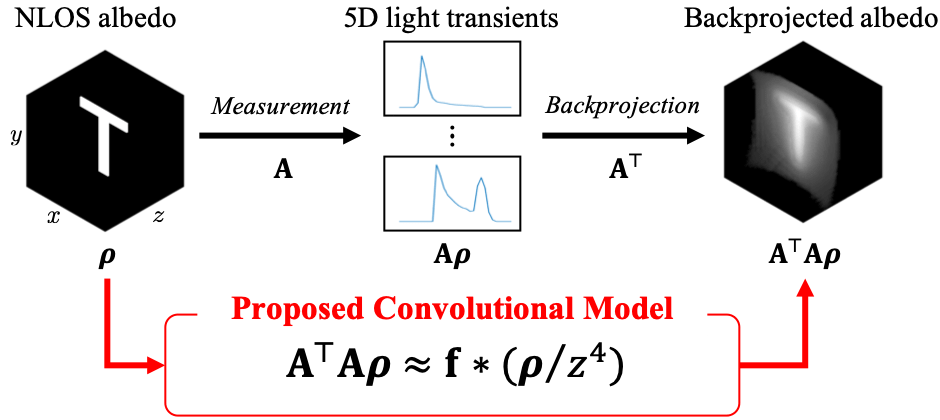
The need for a tractable framework for NLOS imaging

Non-line-of-sight (NLOS) imaging aims to reconstruct scenes outside the field of view of an imaging system. A common approach is to measure the so-called light transients, which facilitates reconstructions through ellipsoidal tomography that involves solving a linear least-squares. Unfortunately, the corresponding linear operator is very high-dimensional and lacks structures that facilitate fast solvers, and so, the ensuing optimization is a computationally daunting task. We introduce a computationally tractable framework for solving the ellipsoidal tomography problem.

Paper

Convolutional Approximations to the General Non-Line-of-Sight Imaging Operator

Our main observation is that the Gram of the ellipsoidal tomography operator is convolutional, either exactly under certain idealized imaging conditions, or approximately in practice. This, in turn, allows us to obtain the ellipsoidal tomography solution by using efficient deconvolution procedures to solve a linear least-squares problem involving the Gram operator. The computational tractability of our approach also facilitates the use of various regularizers during the deconvolution procedure. We demonstrate the advantages of our framework in a variety of simulated and real experiments.



High Efficiency

More Info

We can efficiently obtain the ellipsoidal tomography reconstruction by solving an equivalent linear least-squares involving the Gram operator: As the Gram operator is convolutional, this problem can be solved using computationally-efficient deconvolution algorithms.



Theoretical Justification

More Info

The GRAM operator provides a theoretical justification for the filtered backprojection algorithm: We can show that filtered backprojection corresponds to using an approximate deconvolution filter to solve the problem involving the Gram operators.



Flexibility

More Info

The Gram operator facilitates the use of a wide range of priors to regularize the NLOS reconstruction problem: The convolutional property of the Gram operator implies that the corresponding regularized least squares remain computationally tractable.itor

Simulation Result

Comparing to full linear reconstruction, our method has faster runtime while providing similar reconstruction quality.

Compared with filtered backprojection, our method performs better
even without the use of priors as it uses the exact inverse filter whereas filtered backprojection behaves as a heuristic inverse filter.

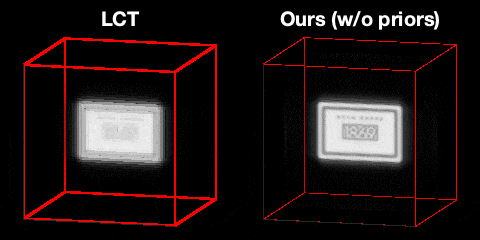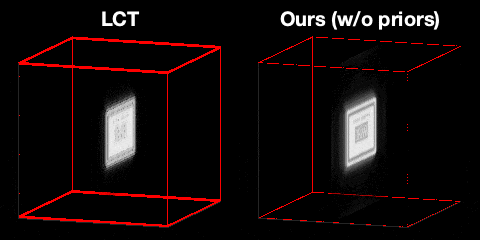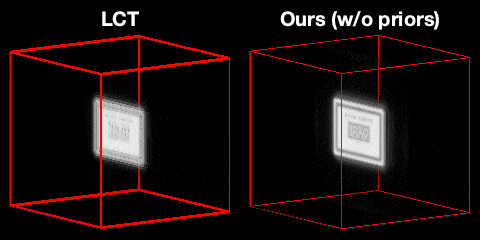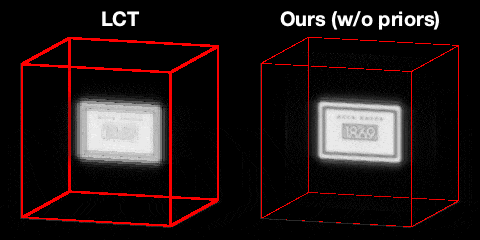
Even though the temporal resolution of the light transient is enough to reconstruct the letters on the soap, it is not reconstructed well in light cone transform (LCT) due to the poor lateral resolution. On the other hand, we can recover significantly higher detail by running the same confocal measurements through our computational pipeline even without any prior.